import torch
import torch.nn as nn

假设你已经定义了一个模型，例如：

class MyModel(nn.Module):
def init(self):
super(MyModel, self).init()
self.fc1 = nn.Linear(10, 50)
self.fc2 = nn.Linear(50, 1)

def forward(self, x):
    x = torch.relu(self.fc1(x))
    x = self.fc2(x)
    return x

创建一个模型实例

model = MyModel()

计算并打印模型的参数个数

def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)

print(f’模型的参数个数: {count_parameters(model)}’)

SGD（随机梯度下降）和反向传播是深度学习训练中两个关键的概念，它们之间是紧密相关的。

1. 反向传播（Backpropagation）：是一种优化算法，用于最小化神经网络的损失函数。其核心思想是通过计算损失函数相对于网络权重的梯度来更新权重。当神经网络进行前向传播时，数据从输入层传递到输出层，并计算出损失（即预测值与真实值之间的差距）。然后，在反向传播阶段，算法通过链式法则计算损失函数关于每个权重的偏导数（梯度），并将这些梯度传播回网络，用于更新权重。

2. SGD（Stochastic Gradient Descent）：是一种优化技术，用于更新神经网络的权重以最小化损失函数。在标准的梯度下降中，你会计算整个训练集的平均梯度来更新权重。然而，当训练集非常大时，这会非常慢。SGD通过在每次迭代中只使用一个样本来估计梯度并更新权重，从而加速训练过程。虽然SGD的权重更新可能更加嘈杂，但它通常能够更快地收敛。

现在来看它们之间的关系：

• 反向传播是用来计算损失函数相对于权重的梯度。
• SGD使用这些梯度来更新权重。

简而言之，反向传播用于计算梯度，而SGD则使用这些梯度来更新神经网络的权重。在深度学习的训练过程中，这两个概念通常是结合使用的，反向传播负责计算出梯度，然后SGD（或其他优化算法，如Adam、RMSprop等）使用这些梯度来更新权重，以最小化损失函数。

如果你想要用三维的方式来画出这个函数的图像，你可以使用plot_surface方法。首先，你需要从mpl_toolkits.mplot3d包中导入Axes3D。这样，你就可以创建一个三维的坐标轴，然后在这个坐标轴上画出你的图像。下面是一个示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 创建数据
x = np.linspace(-50, 50, 400)
y = np.linspace(-50, 50, 400)
X, Y = np.meshgrid(x, y)
Z = 1/20 * X**2 + Y**2

# 创建一个图像和一个三维坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 画出三维的曲面图
ax.plot_surface(X, Y, Z, cmap='viridis')

# 添加标签和标题
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Surface plot of 1/20*x^2 + y^2')

# 显示图像
plt.show()

这段代码将会创建一个三维的曲面图，使用颜色来表示Z值的大小。cmap='viridis'是一个颜色映射选项，你可以根据自己的喜好更改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-50, 50, 400)
y = np.linspace(-50, 50, 400)
X, Y = np.meshgrid(x, y)

Z = 1/20*X**2 + Y**2
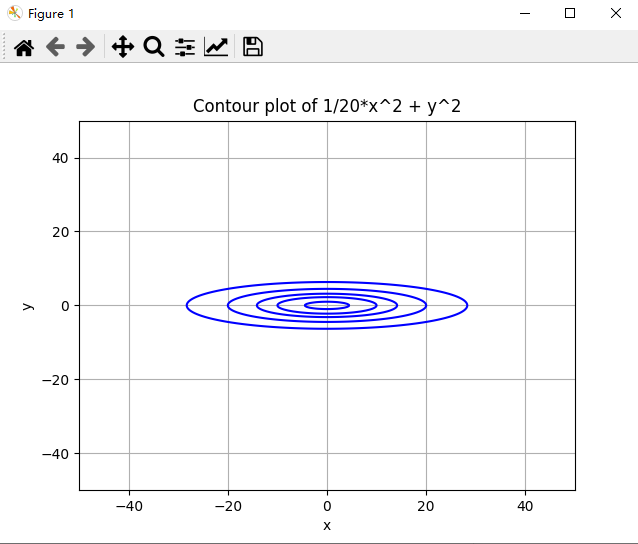
plt.contour(X, Y, Z, levels=[1, 5, 10, 20, 40], colors='b')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Contour plot of 1/20*x^2 + y^2')
plt.grid(True)
plt.show()

这段代码是使用Python语言编写的，其目的是通过matplotlib库绘制函数 1/20*x^2 + y^2 在x和y范围为[-50, 50]内的等高线图。下面是详细解释：

1. import numpy as np：导入numpy库，并简写为np。Numpy是Python中用于处理数组和矩阵的库，常用于数值计算。

2. import matplotlib.pyplot as plt：导入matplotlib.pyplot库，并简写为plt。Matplotlib是Python中一个常用的绘图库，可以创建各种静态、动态、交互式的图表。

3. x = np.linspace(-50, 50, 400)：使用numpy的linspace函数，在-50到50之间创建一个包含400个点的等间距数列，赋值给变量x。

4. y = np.linspace(-50, 50, 400)：与上一行类似，创建另一个在-50到50之间的包含400个点的等间距数列，赋值给变量y。

5. X, Y = np.meshgrid(x, y)：使用numpy的meshgrid函数，根据x和y数组生成一个二维的网格坐标系。X和Y是二维数组，其中X的每个元素表示相应点的x坐标，Y的每个元素表示相应点的y坐标。

6. Z = 1/20*X**2 + Y**2：定义一个二维数组Z，用于存储根据公式 1/20*x^2 + y^2 计算出的每个网格点的z值。

7. plt.contour(X, Y, Z, levels=[1, 5, 10, 20, 40], colors='b')：使用matplotlib的contour函数绘制等高线图。X和Y是网格点的坐标，Z是每个网格点的高度。levels 参数定义了绘制的等高线的高度值，本例中为[1, 5, 10, 20, 40]。colors 参数定义了等高线的颜色，本例中为蓝色（’b’）。

8. plt.xlabel('x')：为图表的x轴添加标签，标签内容为 ‘x’。

9. plt.ylabel('y')：为图表的y轴添加标签，标签内容为 ‘y’。

10. plt.title('Contour plot of 1/20*x^2 + y^2')：为图表添加标题，标题内容为 ‘Contour plot of 1/20*x^2 + y^2’。

11. plt.grid(True)：添加网格线。参数True表示显示网格线。

12. plt.show()：显示图表。这会打开一个窗口展示刚刚绘制的等高线图。

总的来说，这段代码使用numpy和matplotlib库，绘制了函数1/20*x^2 + y^2在x和y范围为[-50, 50]内的等高线图。通过调整参数，我们可以改变图像的分辨率，等高线的值以及其他可视化属性。此图形有助于我们理解函数在二维空间中的形状。特别是，通过这种可视化方式，我们可以很容易地看到函数的高度变化以及它在不同区域的曲率。

在执行这段代码时，你需要确保你的Python环境中已经安装了numpy和matplotlib库。如果没有安装，可以通过pip工具来安装：

1

pip install numpy matplotlib

然后，你可以将这段代码保存为一个.py文件，或在Jupyter Notebook中运行它。如果一切正常，你应该能看到一个展示等高线的窗口。在这个图中，蓝色的线表示函数在不同高度值（1, 5, 10, 20, 40）的轮廓。你还会注意到x轴和y轴都有标签，图表中包含网格线，以及标题说明了图的内容。

这种可视化方法在学习和理解多变量函数时是非常有用的，它可以帮助我们了解函数的形状、极值点以及其他重要特性。

1. 可读性：代码应该易于理解和维护，使用有意义的变量名和注释。
2. 效率：程序需要在合理的时间内完成任务，使用算法和数据结构优化性能。
3. 可靠性：程序应该稳定运行，不会因为输入或环境变化而崩溃。
4. 安全性：程序应该保护用户数据和系统安全，防止恶意攻击和漏洞利用。
5. 灵活性：程序应该具有适应变化的能力，可以扩展和修改功能。
6. 可复用性：程序应该尽可能地重用已有代码和库，减少冗余工作。
7. 可移植性：程序应该能够在不同平台和操作系统上运行，不受限于特定环境。
8. 易于测试：程序的每个功能都应该方便地进行单元测试和集成测试。
9. 易于调试：程序应该能够快速定位和修复bug，提供有用的错误信息和日志。
10. 可扩展性：程序应该能够容易地添加新功能和模块。
11. 可维护性：程序应该设计良好，易于修改和更新，不会产生过多技术债务。
12. 一致性：程序代码应该遵循一致的风格和惯例，便于理解和协作。
13. 可读写性：程序应该能够读取和写入不同格式的数据，支持导入和导出文件。
14. 易用性：程序应该提供友好的用户界面和操作指南，方便用户使用。
15. 科学性：程序应该基于科学原则和实证数据，确保结果准确可靠。
16. 灵敏性：程序应该对用户输入做出及时响应和反馈。
17. 合规性：程序应该符合法律法规和行业标准，保护用户隐私和权益。
18. 可追溯性：程序应该记录关键步骤和结果，便于后续分析和审计。
19. 可定制性：程序应该能够根据用户需求进行个性化设置和配置。
20. 可恢复性：程序应该具有恢复功能，当发生错误或中断时，可以恢复到之前的状态。